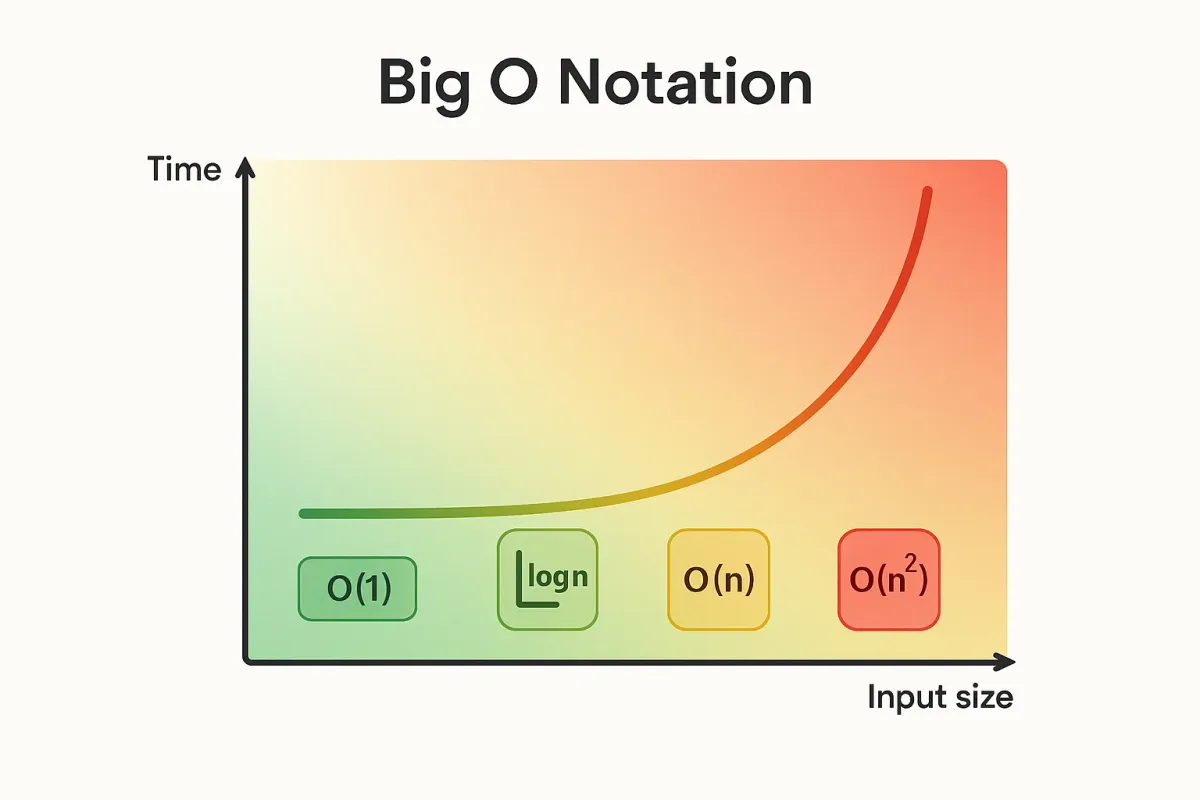
Big O Notation for Beginners: A JavaScript Developer's Guide
Understanding algorithm efficiency and performance analysis
What is Big O Notation?
Big O notation is a mathematical way to describe how the performance of an algorithm changes as the input size grows. Think of it as a report card for your code's efficiency - it tells you how well your algorithm will scale when dealing with larger datasets.
Imagine you're organizing a library. With 10 books, any system works fine. But what happens when you have 10,000 books? Or 1 million? Big O notation helps us predict and compare how different approaches will perform as our data grows.
Why Should You Care?
As a developer, understanding Big O notation helps you:
- Write more efficient code that handles large datasets gracefully
- Make informed decisions when choosing between different algorithms
- Optimize bottlenecks in your applications
- Ace technical interviews where Big O questions are common
- Debug performance issues more effectively
The Most Common Big O Complexities
Let's explore the most important Big O complexities with practical JavaScript examples:
O(1) - Constant Time
"No matter how big the input, it takes the same amount of time"
// Accessing an array element by index
function getFirstElement(array) {
return array[0]; // Always takes the same time
}
// Getting object property
function getUserName(user) {
return user.name; // Instant lookup
}
// Mathematical operations
function addNumbers(a, b) {
return a + b; // Same speed regardless of number size
}
console.log(getFirstElement([1, 2, 3])); // O(1)
console.log(getFirstElement([1, 2, 3, ...1000000])); // Still O(1)Real-world analogy: Like having a bookmark in a book - you can instantly flip to that page regardless of how thick the book is.
O(n) - Linear Time
"As input doubles, time roughly doubles"
// Searching through an array
function findNumber(array, target) {
for (let i = 0; i < array.length; i++) {
if (array[i] === target) {
return i;
}
}
return -1;
}
// Printing all elements
function printAllItems(items) {
items.forEach(item => {
console.log(item); // We visit each item once
});
}
// Summing array elements
function sumArray(numbers) {
let total = 0;
for (const num of numbers) {
total += num; // One operation per element
}
return total;
}
const smallArray = [1, 2, 3]; // 3 operations
const largeArray = [1, 2, 3, ...1000]; // 1000 operations
Real-world analogy: Reading every page of a book to find a specific quote - twice as many pages means twice as much reading.
O(n²) - Quadratic Time
"Nested loops are the usual culprit"
// Comparing every element with every other element
function findDuplicates(array) {
const duplicates = [];
for (let i = 0; i < array.length; i++) {
for (let j = i + 1; j < array.length; j++) {
if (array[i] === array[j]) {
duplicates.push(array[i]);
}
}
}
return duplicates;
}
// Bubble sort algorithm
function bubbleSort(array) {
const arr = [...array]; // Create a copy
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap elements
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}
// Matrix operations
function multiplyMatrices(matrixA, matrixB) {
const result = [];
for (let i = 0; i < matrixA.length; i++) {
result[i] = [];
for (let j = 0; j < matrixB[0].length; j++) {
result[i][j] = 0;
for (let k = 0; k < matrixB.length; k++) {
result[i][j] += matrixA[i][k] * matrixB[k][j];
}
}
}
return result;
}
Real-world analogy: Comparing every person in a room with every other person to find couples - double the people means four times the comparisons!
O(log n) - Logarithmic Time
"Divide and conquer - very efficient!"
// Binary search (array must be sorted)
function binarySearch(sortedArray, target) {
let left = 0;
let right = sortedArray.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (sortedArray[mid] === target) {
return mid;
} else if (sortedArray[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
// Finding height of a balanced binary tree
function findTreeHeight(node) {
if (!node) return 0;
const leftHeight = findTreeHeight(node.left);
const rightHeight = findTreeHeight(node.right);
return Math.max(leftHeight, rightHeight) + 1;
}
const sortedNumbers = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19];
console.log(binarySearch(sortedNumbers, 7)); // Found in ~3 steps instead of 7
Real-world analogy: Finding a word in a dictionary by opening to the middle and eliminating half the pages each time.
O(n log n) - Linearithmic Time
"The sweet spot for efficient sorting"
// Merge Sort - divide and conquer
function mergeSort(array) {
if (array.length <= 1) return array;
const mid = Math.floor(array.length / 2);
const left = mergeSort(array.slice(0, mid));
const right = mergeSort(array.slice(mid));
return merge(left, right);
}
function merge(left, right) {
const result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
return result
.concat(left.slice(leftIndex))
.concat(right.slice(rightIndex));
}
// Quick Sort implementation
function quickSort(array) {
if (array.length <= 1) return array;
const pivot = array[array.length - 1];
const left = array.filter(item => item < pivot);
const right = array.filter(item => item > pivot);
return [...quickSort(left), pivot, ...quickSort(right)];
}
const unsorted = [64, 34, 25, 12, 22, 11, 90];
console.log(mergeSort(unsorted)); // [11, 12, 22, 25, 34, 64, 90]
Practical Examples: Optimizing Real Code
Example 1: Finding Common Elements
// ❌ Inefficient O(n²) approach
function findCommonElementsSlow(array1, array2) {
const common = [];
for (const item1 of array1) { // O(n)
for (const item2 of array2) { // O(m)
if (item1 === item2 && !common.includes(item1)) {
common.push(item1); // includes() is also O(n)!
}
}
}
return common;
}
// ✅ Efficient O(n + m) approach using Set
function findCommonElementsFast(array1, array2) {
const set1 = new Set(array1); // O(n)
const common = [];
for (const item of array2) { // O(m)
if (set1.has(item)) { // O(1) lookup!
common.push(item);
set1.delete(item); // Prevent duplicates
}
}
return common;
}
Example 2: Counting Character Frequency
// ❌ Slow approach O(n²)
function countCharactersSlow(string) {
const result = {};
for (const char of string) { // O(n)
const count = string.split(char).length - 1; // O(n) for each char!
result[char] = count;
}
return result;
}
// ✅ Fast approach O(n)
function countCharactersFast(string) {
const result = {};
for (const char of string) { // O(n)
result[char] = (result[char] || 0) + 1; // O(1) operations
}
return result;
}
console.log(countCharactersFast("hello world"));
// Output: { h: 1, e: 1, l: 3, o: 2, ' ': 1, w: 1, r: 1, d: 1 }
Common Pitfalls and How to Avoid Them
Pitfall 1: Hidden Nested Loops
// ❌ This looks like O(n) but it's actually O(n²)
function removeDuplicatesWrong(array) {
return array.filter((item, index) =>
array.indexOf(item) === index // indexOf is O(n)!
);
}
// ✅ True O(n) solution
function removeDuplicatesRight(array) {
return [...new Set(array)]; // Set operations are O(1) on average
}
Pitfall 2: Unnecessary Operations in Loops
// ❌ Recalculating length every iteration
function processArrayWrong(array) {
for (let i = 0; i < array.length; i++) { // length calculated each time
// Process array[i]
console.log(array[i]);
}
}
// ✅ Cache the length
function processArrayRight(array) {
const length = array.length; // Calculate once
for (let i = 0; i < length; i++) {
console.log(array[i]);
}
}
Space Complexity: Don't Forget Memory!
Big O also applies to memory usage:
// O(1) space - uses same amount of memory regardless of input
function findMax(array) {
let max = array[0];
for (let i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
return max;
}
// O(n) space - creates new array of same size
function doubleArray(array) {
return array.map(x => x * 2);
}
// O(n) space - recursive calls use stack memory
function fibonacci(n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2); // Each call uses stack space
}
Performance Testing in Practice
Here's how to measure and compare algorithms:
function measurePerformance(fn, input, label) {
const start = performance.now();
const result = fn(input);
const end = performance.now();
console.log(`${label}: ${end - start} milliseconds`);
return result;
}
// Test different sorting algorithms
const largeArray = Array.from({length: 10000}, () =>
Math.floor(Math.random() * 10000)
);
measurePerformance(bubbleSort, [...largeArray], "Bubble Sort O(n²)");
measurePerformance(mergeSort, [...largeArray], "Merge Sort O(n log n)");
measurePerformance(array => [...array].sort((a, b) => a - b), [...largeArray], "Native Sort");
Quick Reference: Time Complexity Cheat Sheet
| Operation | Array | Object | Set | Map |
|---|---|---|---|---|
| Access | O(1) | O(1) | - | - |
| Search | O(n) | O(1) | O(1) | O(1) |
| Insert | O(n) | O(1) | O(1) | O(1) |
| Delete | O(n) | O(1) | O(1) | O(1) |
Key Takeaways
- O(1) is ideal - Constant time operations are your best friend
- O(log n) is great - Logarithmic algorithms scale beautifully
- O(n) is acceptable - Linear time is often unavoidable and fine
- O(n log n) is good - The best we can do for comparison-based sorting
- O(n²) is concerning - Avoid nested loops when possible
- O(2ⁿ) is alarming - Exponential algorithms don't scale
Practice Problems
Try optimizing these common scenarios:
- Find the intersection of two arrays (aim for O(n + m))
- Check if a string is an anagram of another (aim for O(n))
- Find the most frequent element in an array (aim for O(n))
- Implement a function to reverse a string (aim for O(n) time, O(1) space)
Conclusion
Big O notation isn't about making your code perfect from day one - it's about making informed decisions. When you're dealing with small datasets, the difference between O(n) and O(n²) might be negligible. But as your application grows and handles more data, these choices become critical.
Start by recognizing the patterns (nested loops = O(n²), single loops = O(n), direct access = O(1)), and gradually develop an intuition for writing efficient code. Your future self (and your users) will thank you!
Remember: Premature optimization is the root of all evil, but understanding efficiency is the root of all scalable software.
Happy coding! 🚀